北京培峰技术有限责任公司官方网站!
英文站


新闻中心
两相流:在气体管道模拟中考虑液体的存在
访问量:
51
在陆上和海上作业的天然气收集和输送管道中,气体的多相流动和液体的低负荷经常发生。文献和实验研究表明,当气体和少量液体同时在管道中流动时,可以得到分散的液滴和分层的流动模式。对于这些系统的持力和压降预测,几乎没有相关性,而且很少给出令人满意的结果。对直径从1英寸到3英寸不等的小直径塑料和钢水平管道中流动的气油和气水系统进行了实验研究。实验在伦敦帝国理工学院和加拿大卡尔加里大学的多相流实验室进行。还评估了实际运行中输送少量碳氢液体的天然气管道系统的数据。根据实验结果和运行数据,提出了两种建模方法:


1)、 一种均匀的方法,非常低的液体负荷(持有量高达0.005),典型的气体传输系统。针对这种流动状态,建立了基于阻力的摩擦系数相关关系。
2)、 一种机械分层两相方法,用于较高的液体负荷(大于0.005),通常存在于气体收集系统中,并考虑到:
a. 可用流动面积的减少和液体薄膜润湿管道周边的程度。观察到气液界面是平坦的或弯曲的。
b. 液膜与气体的界面摩擦因数。基于液体和气体雷诺数以及膜厚和保持叩,建立了一种新的相关性。这种相关性已经成功地测试了实验和实际管道操作数据。
介绍
管道中的气体和液体的联合流动在化学工艺工业中很常见,特别是石油和天然气管道流动。在过去的50年里,人们提出了许多理论和关联来预测管道中的压降和液体滞留量。然而,在多相气-液流中,它们都没有给出一致可靠的结果。
输送气体和低负荷液体的系统可能是多相历史上研究最少的系统之一,因此这些系统的文献和数据是有限的。在石油工业中,这种现象经常发生在天然气集输管道和陆上、近海作业中。伴随的液体通常是重烃组分和水,可以从几个来源引入。来自压缩设施的液体(例如。润滑油)和处理厂(例如。乙二醇)以及逆行冷凝的产物可能伴随着气体在运输过程中。储层中的一些水也可能导致液体负荷。
伴随的液体影响系统的运输效率。大多数收集管道(通常每百万立方英尺气体(bbls/MMSCF)的液体负荷高达100桶)作为多相组分输送流体。设计这些管道将需要准确和充分地预测液体的含率和相应的压降,这与气液混合物的物理和热力学性质一致。对于输送管道,液体夹带通常小于10bbls/MMSCF的气体,大多数管道公司通常采用“干气”模型来预测系统的输送能力。在现实中,伴随的液体可能以薄膜的形式传播,也可能以分散的液滴在主要气相中分布(Gould等人,1975年;HopeEtal,1977年)。薄膜和液滴都阻碍了气体通过管道的流动。一些管道公司,根据液体浓度水平,通过调整传输或效率因素来校准他们的系统,以考虑由于伴随的液体而产生的额外阻力。目前的单相建模方法不足以预测移动这些流体混合物所需管道的运输能力。虽然单相气体和单相液体管道的设计原则已经牢固确立,但两相(或多相)设计仍在不断发展,需要大量的实验验证。在本研究中,采用均匀(伪单相)和两相分层流动方法来描述管道中气体和低负荷液体系统的行为和输运特性。均匀模型对于分散相情况是足够的,而分层流动情况则需要一种分离的流动方法。
-
问题陈述
正在研究的问题如下:
a. 量化伴随液体在气体和低负荷液体联合输送过程中对管道摩擦因数和压降的影响。
b. 确定液相的输送方式
c. 以识别从一个流模式到另一个流模式的转换点
d. 确定适用的流体-壁面和界面摩擦因子
-
现有的解决办法
现有的解决办法同时考虑单相和两相方法。
2.1 现有的单相方法。
现有的描述这两相现象的单相方法通常是基于操作数据来研究管道粗糙度或效率的修改。还需要对操作流动状况以及流体对壁面剪应力(或摩擦系数)作出适当的定义。
2.2 单相流动摩擦系数预测
摩擦系数的定义一直是流体动力学研究人员争论的焦点。在确定的流动状态的基础上,各种研究人员提出了不同的摩擦因子相关性来表征流体的单相流动。对于小直径管道(通常用于实验室),Blasius型表达式,如Taitel和Dukler(1976)提出的表达式,通常是摩擦因子的一个很好的近似。因此

其中f是摩擦因数,a和b是常数,Re是雷诺数。对于操作管道,文献中给出了单相摩擦因数的各种形式,表1给出了一些著名的摩擦因数。摩擦因数通常用传递因数来表示,它反映了气体通过管道的传递程度,是一个重要的操作指标。传递因数表示为摩擦因数的逆平方根。
表1-单相流动的传输因子(Uhl,1965)
方程式 传输因数 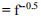
光滑的管道方程 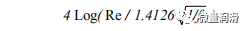
粗管方程 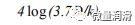
W形口 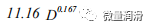
A形锅柄 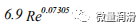
B形锅柄 
Colebrook White公式 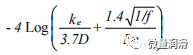
AGA部分湍流 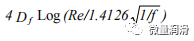
AGA完全湍流 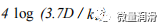
2.3 压降预测-单相流
用于计算管道压力损失的方程是由动量守恒(牛顿第二运动定律)导出的,它将物体的动量变化率与作用在物体上的外力之和联系起来。1935年,美国矿业局提出了一般流动方程(Uhl,1965),作为稳态干气流的压降预测方程。该方程是由下面给出的伯努利方程发展而来的

其中Hi是一个点的高程,Le代表能量损失。
一般流动方程的通常形式如下:
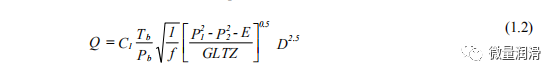
其中:
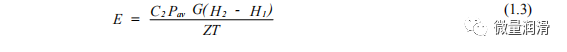
在推导一般流动方程时,提出了以下假设:
i). 沿管道长度流动平稳。
ii). 流动假定为等温流动。
iii). 假定气体的压缩性具有恒定的平均值。
iv). 线中的动能变化假定可以忽略不计,因此排除动能项。
v). 假定流动速度用表观体积平均速度精确表征。
vi). 假设摩擦因数沿管段恒定。
vii). 假定压力随高程的变化是平均截面压力下某一恒定平均密度的消失。
viii). 由于涡流和其他流动不规则而造成的损失被忽略。
-
现有的多相流方法
气体和低负荷液体系统的多相方法考虑了均匀流动和分层流动分析。
3.1 均匀流
均匀模型将气液混合物视为具有平均流体性质的伪单相。流体性质(密度和粘度)的适当定义对模型的准确性至关重要。过去在均匀情况下广泛使用的方法是将两相混合物的守恒方程写成具有经验定义的密度和粘度混合性质的单相流体。因此,得到的混合模型仅由三个混合守恒方程组成。守恒方程组解相对简单,并与相应的单相流相似。然而,混合模型不能充分考虑相之间质量、动量和能量交换的动力学。偏离热平衡和平均速度之间的差异可能存在。混合性质表示为气体和液体性质以及它们各自的保持率的函数。摩擦因数通常表示为雷诺数的函数,用混合性质来定义。下面给出了混合性能pm和(密度和粘度)的最常用表达式。
混合物密度
混合密度表示为:

混合物粘度相关性
均匀流动常用以下混合粘度相关性:

x是气体的重量分数
式中CL为液体输入体积分数
所有这些相关性都是经验的,在一致预测其他系统的混合物粘度方面并不可靠。
3.2 压降预测-均匀流动
均相流的压降评价与单相流的评价相似,只是在确定摩擦因子时使用了混合流体性质。Beggs&Brill(1973)和Dukler(1964)混合摩擦因子关联式在天然气工业中被广泛应用于均相流的压降预测。混合摩擦系数fm由Beggs和Brill(1973)AS给出
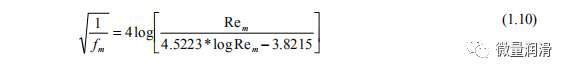
其中REM混合雷诺数,并由

杜克勒等人(1964)的混合摩擦因子表达式,FM如下:
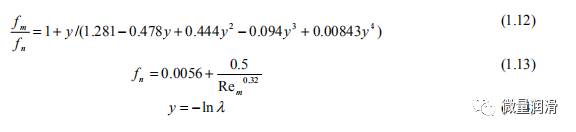
流体性质表示
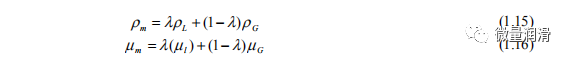
在那里,λ,无滑移保持是作为

霍普等人(1977年)对气体和液体的同时流动和低负荷进行了最重要的均匀评估)。他们将三个著名的单相气体方程(AGA、Colebrook-White和Panhandle)与三个双相模型进行了比较(Baker等人,1954年;Dukler,1964年和Beggs&Brill,1973年)。他们预测了一条北海管道的压降,该管道输送约900MMSCF的气体,液体负荷为5bbls/MMSCF的气体。单相模型比两相模型给出了更好的预测,AGA相关性是迄今为止最好的单相模型。Ullah(1987)对西印度群岛沿海的湿气体系统(1bbl液体/MMSCF气体)进行了类似的分析,并得出了类似的结果。
在先前的一项工作中,Gould和Ramsey(1975年)研究了一条NPS16管道,输送气体的液体负荷为10-20bbls/MMSCF,并报告了与Hope等人(1977年)和Ullah(1987年)相反的结果)。他们根据墨西哥湾沿岸的数据测试了Beggs和Brill相关性以及PanhandleB方程,并得出结论,Beggs和Brill相关性比单相(Panhandle)模型提供了更好的预测。Flanigan(1958)还将各种流动状态下的液体负荷与PanhandleB效率因子相关,但忽略了下坡段的压力恢复。然而,他的工作提供了一个一级近似的低负荷液体对压降的影响。
在所有这些研究中(除了Hope和Nelson,1977),摩擦因子被表示为雷诺数的函数。虽然这可能足以用于实验管道(如Blasius方程),但对于流动可能以管道粗糙度为主的操作管道,可能会发生明显的误差。
3.3 分层流动法
大多数管道公司继续调整效率系数和有效粗糙度,以考虑均匀模式流动中的非理想性,但不清楚这种“修正”单相方法是否适合限制液体负荷。当相表现出非常不同的流动特性时,可能需要多相分层流动方法。尽管过去50年来对多相流进行了大量的研究和进展,但关于涉及气体和低负荷液体的系统的文献和数据仍然有限。现有的两相模型大多过于经验性和“数据特异性”,无法充分描述气体和低液体负荷的流动行为。现有两相模型的另一个明显的缺点是,它们一致地将摩擦因数表示为雷诺数的函数。可能不是这样。从单相气体运行数据可以看出,在高流量(即雷诺数)下,雷诺数可能对摩擦因子或气体传输因子影响很小或没有影响。完全粗糙的流动)。与均匀方法不同,分层方法分别处理相,具有不同的物理和热力学性质。相之间的质量、动量和能量转移是显著的,界面相互作用用适当的封闭律来描述。大多数分层模型也假设压力在横截面上是均匀的,并且在每个阶段都是相等的。这种假设有时是合理的,因为观察到径向压差通常很小,在大多数情况下无法测量。然而,这并非普遍接受。由于重力或表面张力的影响,这两个阶段的压力可能有很大的不同。对于气体和低液体负荷系统,Grolman等人(1997)已经证明了这一假设是合理的。现象学概念依赖于流动模式,有时叠加在分层方法上,以充分描述气液流动行为。事实证明,这提供了更好的普遍预测,因为它们描述了“现象”(或机制),而不仅仅是相关的经验数据。
对于分层两相模型,通常采用修正的Taitel-Dukler方法。根据界面的几何形状,可以发生两种类型的分层流动:分层平坦和分层弯曲。分层程度主要由气体和液体的相对速率驱动。对于低气体流量,界面通常是平坦的。对于高气体流量,出现滚波和表面显著的涟漪(Govan,1990年),气液界面经常是弯曲的(Hart和Hammersma,1987年)。洛克哈特和马丁内利的作品(1949年)和后来的泰特尔和杜克勒的贡献(1976年)被普遍认为是分层流动研究的第一个基石。其他重要贡献是Govier和Aziz(1972)的工作,他们用几何模型求解了一维动量方程。
对于分层流动,通常需要定义润湿面积,界面摩擦,流体-壁面摩擦和保持来确定压降。大多数这些参数的定义可能因模型而异。
3.4 界面摩擦因子
定义两相分层流动最重要的参数之一是界面摩擦因子,其定义在两相文献中是众多的。气体在气液界面上的流动会引起液体表面的波或波纹,这对流动提供了一些阻力。界面的几何本质上定义了流动状态和相关的传输机制。本质上,这种两相现象可以看作是一个以运动边界为界的单相系统(Ishii,1984;Grolman等人,1997)和管壁。因此,两相问题可以用具有适当壁面和界面边界条件的单相流动本构方程来描述。许多作者在气液边界界面应力的充分表示上仍然存在分歧。现有的关联式大多将界面摩擦因数表示为下列参数的任意或组合的函数:气体雷诺数、液体雷诺数、保持、表面气体和液体速度以及薄膜厚度或高度。大多数相关性都是经验的,并且基于高于本研究中考虑的液体负荷。此外,这些相关性中的大多数假设界面是平坦的,而不是为本研究的大多数流动条件获得的周向界面。
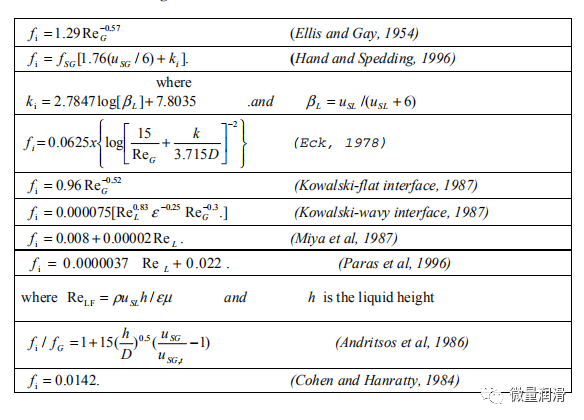
现有的一些界面摩擦因子相关性如表2所示。
表2一些现有的界面摩擦因子相关性
3.5 均匀流动和分层流动之间的过渡
对实验数据的研究表明,在低液体负荷下,持液率是从均匀流动向分层流动过渡的关键因素。在所有情况下,观察到在0.005-0.006之间的行为发生了戏剧性的变化。停留在0.005以下的流动状态,在那里没有观察到明显的薄膜被认为是雾流。高于0.005,流量被认为是分层的。然后在Mandhane等人的地图上表示这两组数据。曼丹等人的地图(以及Taitel和Dukler地图,1976年)表明,在非常低的液体速率(接近于零)和20m/s或以下的浅层气体速度下,流动模式是分层的。这与本研究和其他人的研究结果相反(Paras等人,1994年;Ullah,1978年;Hope和Nelson,1977年)。此外,这些流图归类为环形/环形雾的数据范围非常广泛,似乎包括Hart和Hammersma,1989年;Grolman和Fortuin,1996年;Spedding和Hand,1997年的类似研究中指出的一些分层流动行为。造成这些差异的原因是,Mandhane和Taitel和Dukler地图都是从高液体负荷数据中绘制的,并将其外推到低液体负荷区域。由于现有设备的局限性,在本研究中难以确定分层平坦和分层弯曲之间的视觉区别。哈特和Hammersma的研究(1989)使用高速摄影来确定分层弯曲界面的极限持液量(0.06。因此,对于0.06或更少的搁置,界面被认为是弯曲的,超过0.06,它被认为是平坦的。
基于这些观察,本研究的实验数据分为三组:
a) 含阻0.005或以下的均匀数据;
b) 含阻0.005<含阻的分层曲面界面数据<0.06
c) 含阻的分层平面界面数据>0.06
拟建模型
该模型的关键组成部分是一个具有代表性的摩擦因子的定义,它反映了气体和低负荷液体在管道中同时流动的系统的行为。根据实验数据和现有文献,提出了一种综合均匀分层流动模型来确定该系统的复合摩擦系数。该模型由以下两个分量相关性组成:
-
同质相关
-
两相分层流相关
a) 平面界面和
b) 曲面界面
第3.4节中描述的从均匀到分层的过渡发生在0.005,而从弯曲界面到平面界面的过渡发生在0.06(Hart和Hammersma,1989)。图1中给出的流程图说明了流程状态和转换。
图1流程图
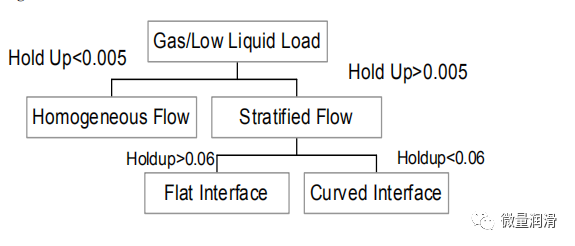
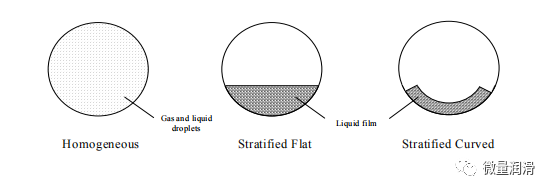
图2显示了该系统横截面积的简化示意图。液相的分布决定了流型是均匀的还是分层的。
图2管道中流动气体和低负荷液体的交叉截面
1、 均相流型
调整单相光滑管道方程,以考虑均匀气体流动和低负荷液体中的液体含量。建立了下面方程2.1中给出的形式的关系
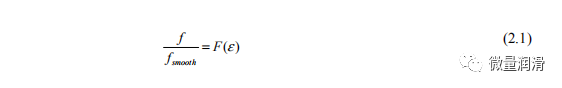
其中fsmooth是表2.1中给出的光滑管道方程,F(ε)是基于液体含率的未知相关函数,ε。分析表明,f/fs光滑与持度之间存在很强的线性关系:
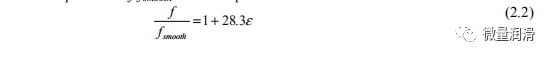
方程2.2表示对均匀气体流动和低负荷液体的光滑管道方程的修正。除了给出零液容的光滑管流的精确表示外,这个方程还允许外推到更高的雷诺数流动。在其他数据集上进行测试时,与广泛使用的Beggs&Brill(绝对误差260%)和Dukler(绝对误差750%)的两相均相表达式的预测相比,这种相关性提供了7%的平均绝对误差%)
对于雷诺数为40,000<Re<10万的系统,还建立了摩擦系数相关关系。
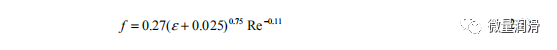
采用爱因斯坦粘度方程计算混合雷诺数。它提供了比1.3.1节中所示的先前表达式更好的预测。混合粘度的定义对均匀摩擦系数有显著影响。现有的Beggs&Brill和Dukler关联式使用Bankoff表达式,它给出了比爱因斯坦方程更高的混合粘度。
2、 两相分层流动模型
分层流动模型在两个关键方面与均匀模型不同:
a) 由于液体滞留而减少的流动横截面积
b) 由于气/液界面上的波或波纹而引起的界面剪切
因此,分层流动是由管壁和粗糙的气液界面为界的连续气体流动来表示的。对于分层的两相解,需要一组修正的Taitel-Dukler方程。质量和动量守恒方程是为无流体加速度的稳定、均匀流动编写的:
质量连续性
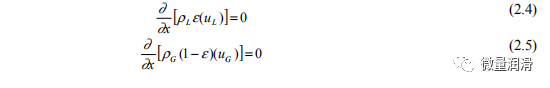
动量守恒
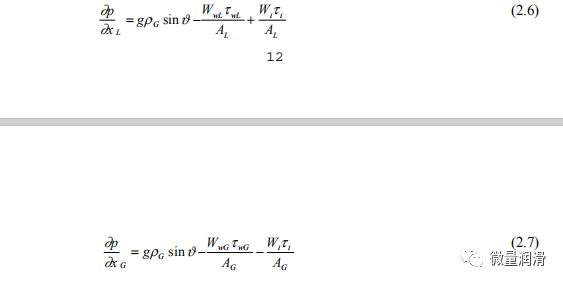
假设气相和液相的压力均匀(Paras等人,1994年;Spedding和Hand,1996年),动量方程可以简化为:
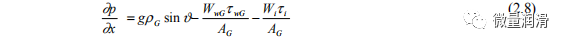
其中

因此,压降可以评估如下:
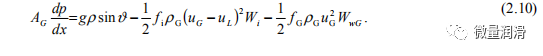
其中
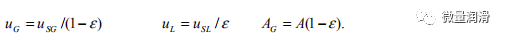
和
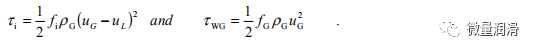
液含量
在本研究中没有建立液体保持相关性。采用Hart和Hammersma(1987)的相关性,为测量数据提供了很好的拟合。他们建议根据表面速率、液体雷诺数和流体密度对液体滞留量进行如下评价:
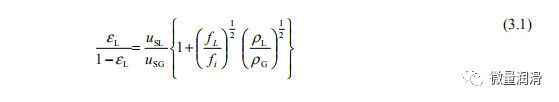
他们从实验中确定了fL/fI的比值

最后的表达
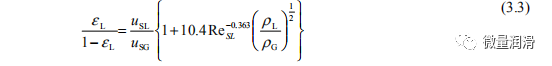
气对水摩擦系数
气壁摩擦系数的确定与单相流动的情况一样。这种单相法在分层流动中的应用是新的。事实上,所有现有的分层流动模型都一致地将摩擦因数表示为雷诺数的函数(Hart和Hammersma,1989年;Baker等人,1988年;Beggs和Brill,1972年;Gregory和Aziz,1972年)。然而,从理论(Schlichting,1968)和单相气体管道的运行数据(Uhl,1965;Hope和Nelson,1988)来看,存在一个临界雷诺数,超过这个临界雷诺数,摩擦因子对雷诺数不敏感,只随管道粗糙度而变化。这两种流动状态被识别:雷诺数相关流动,部分粗糙流动和粗糙度主导流动,完全粗糙流动。对于完全粗糙(湍流)的流动,其中粘性效应可以忽略不计:
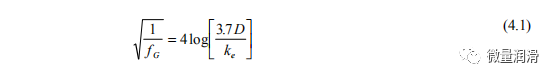
对于部分粗糙(湍流),粘性效应变得显著,相应的表达式是
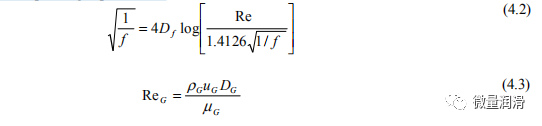
其中µG气体和DG的粘度=4AG/(WG 是气体的水力直径。
摩擦因数也可以用Colebrook-White方程来表示,它将部分粗糙和完全粗糙的分量结合起来,如下所示:
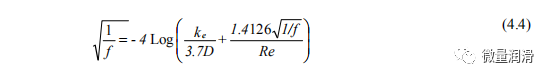
湿分数的测定
对于在高度hL和速度uL的液体层顶部以速度uG流动的光滑分层气体流动,界面通常是平坦的。该气体占据一个横截面积AG与管壁周长WG和液体/气体界面周长Wi。液体的横截面积用AL表示,其管壁周长为WL。
从Taitel和Dukler的分析来看,壁面和界面周长与顶角γ有关,如下所示:
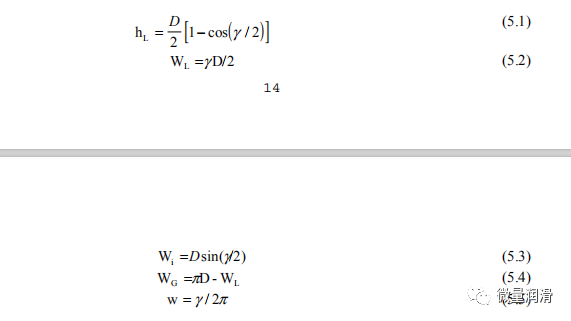
其中
hL是液体高度或深度,
WL是液体润湿壁周长
WG是气体润湿壁周长
Wi是界面周长
w是液体润湿分数的周长。
如果深度hL是输入参数而不是角度γ,则:
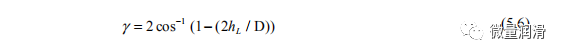
对于弯曲界面,液体保持率、ε和周长与顶角有关γ如下:
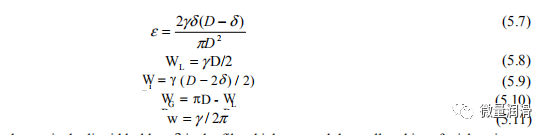
其中ε是液含率,δ是膜厚,壁和界面周长是上面定义的。
采用Hart和Hammersma(1989)的润湿分数近似。他们提出以下等式:

其中Fr是Froude数,表示为:
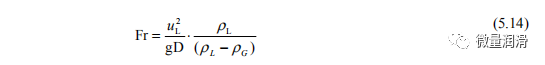
实验得到了C2=0.26的值。
界面摩擦因子
界面摩擦系数是分层流动分析的关键参数之一。界面摩擦因数可由动量守恒方程(Kowalski,1987)确定)。已经发表了一些关于界面摩擦因子的相关性,并在前面的章节中进行了回顾。根据实验结果和现有文献,界面摩擦因子FI与液体雷诺数、气体雷诺数、液体保持率和薄膜高度或厚度相关。界面的几何形状决定了薄膜厚度(弯曲界面)还是薄膜高度(平面界面。对于弯曲界面Hart和Hammersma(1989)提出的确定薄膜厚度的建议。采用统计分析来选择相关参数的最佳组合,以提供最佳的数据拟合和更好的普遍适用性。因此,随着四个无量纲组的确定,对它们的组合进行了评估和测试,以选择最佳的相关性。考虑了1参数、2参数、3参数和4参数表达式。数据中的散点通常从单参数相关性下降到4参数相关性。不同浅层气速和浅层液速的气含率和气雷诺数相关性显示出一致的趋势。这些趋势证实了Holdup和气体雷诺数是必要的参数,但它们本身不足以获得良好的相关性。双参数组合略优于1参数相关性,但也表现出相当大的散射,并给出了较差的预测。三参数组合对实验数据的拟合几乎与四参数相关相同,但绝对误差较大。此外,三参数相关性不完全符合独立数据集和四参数方程。因此,选择4参数相关性作为最佳拟合,并在下面给出。
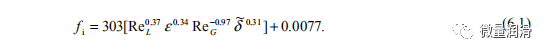
同样的方法用于分层平坦界面。
与分层曲线情况一样,下面给出的4参数相关(方程6.2)为数据提供了最佳拟合,并且具有最小的绝对误差。
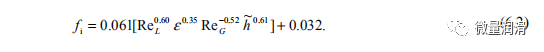
两相摩擦/传输因子
两相摩擦因数由下述决定

然后可以确定两相传输因子为:

模型检验
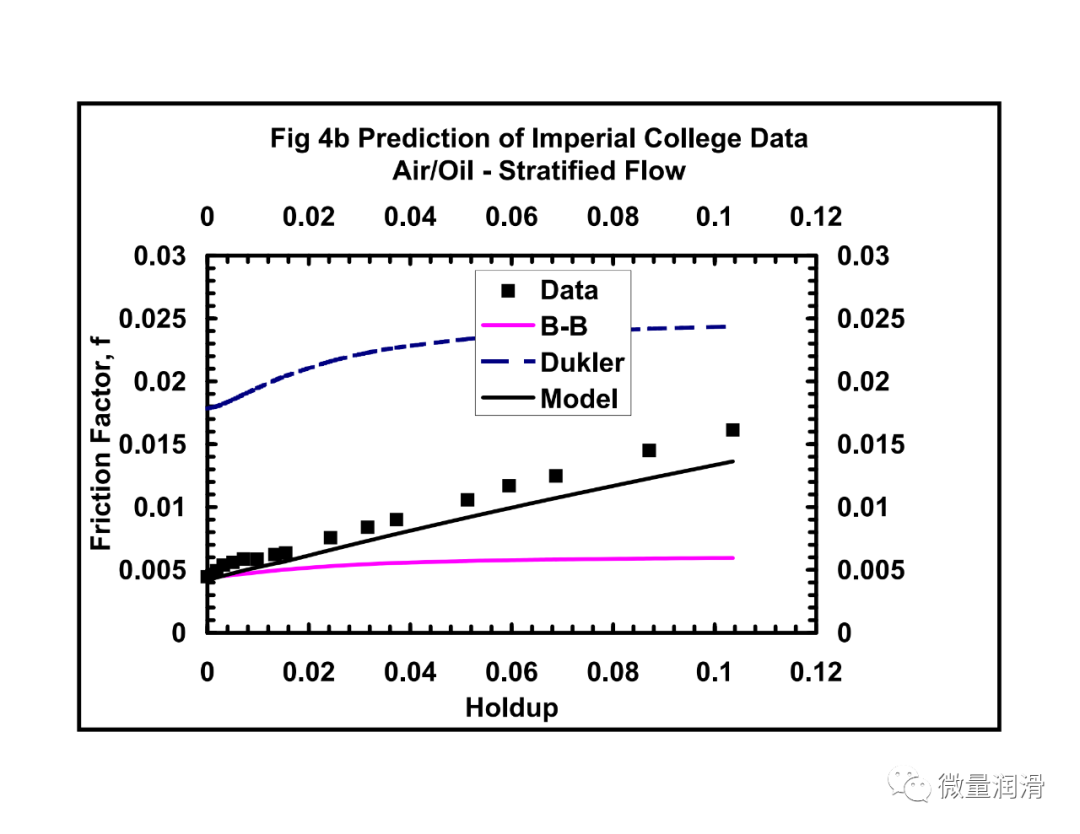
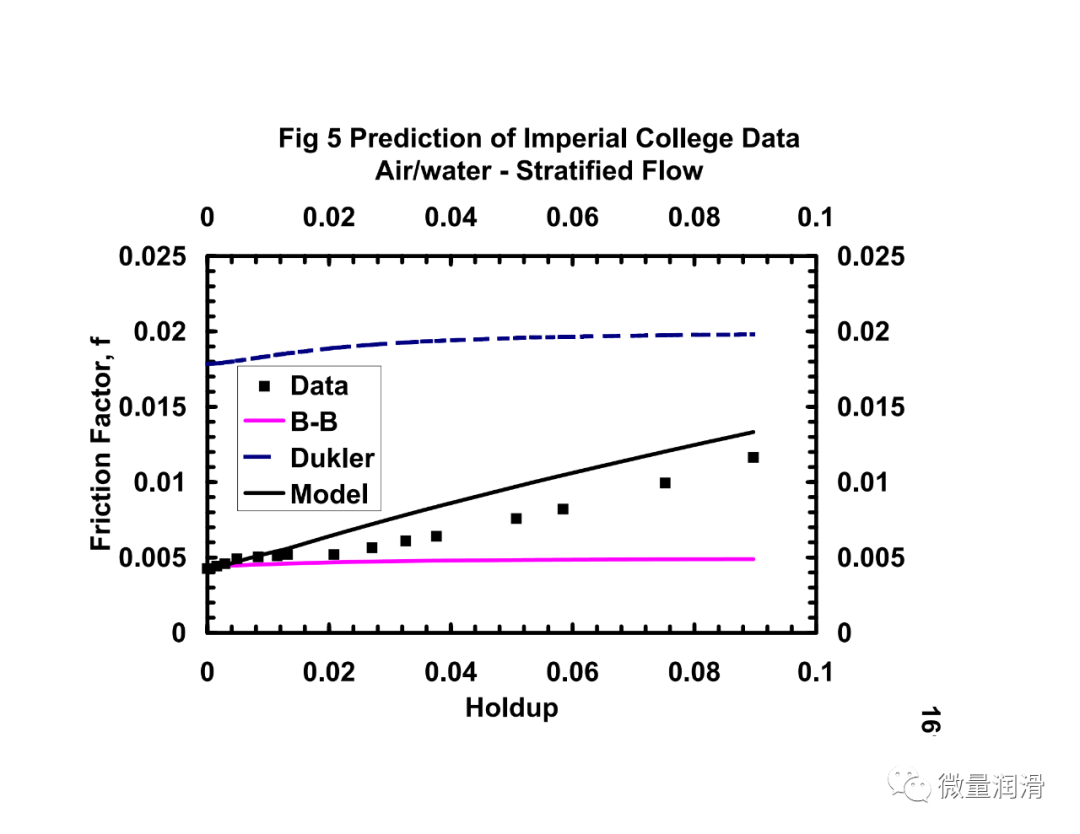
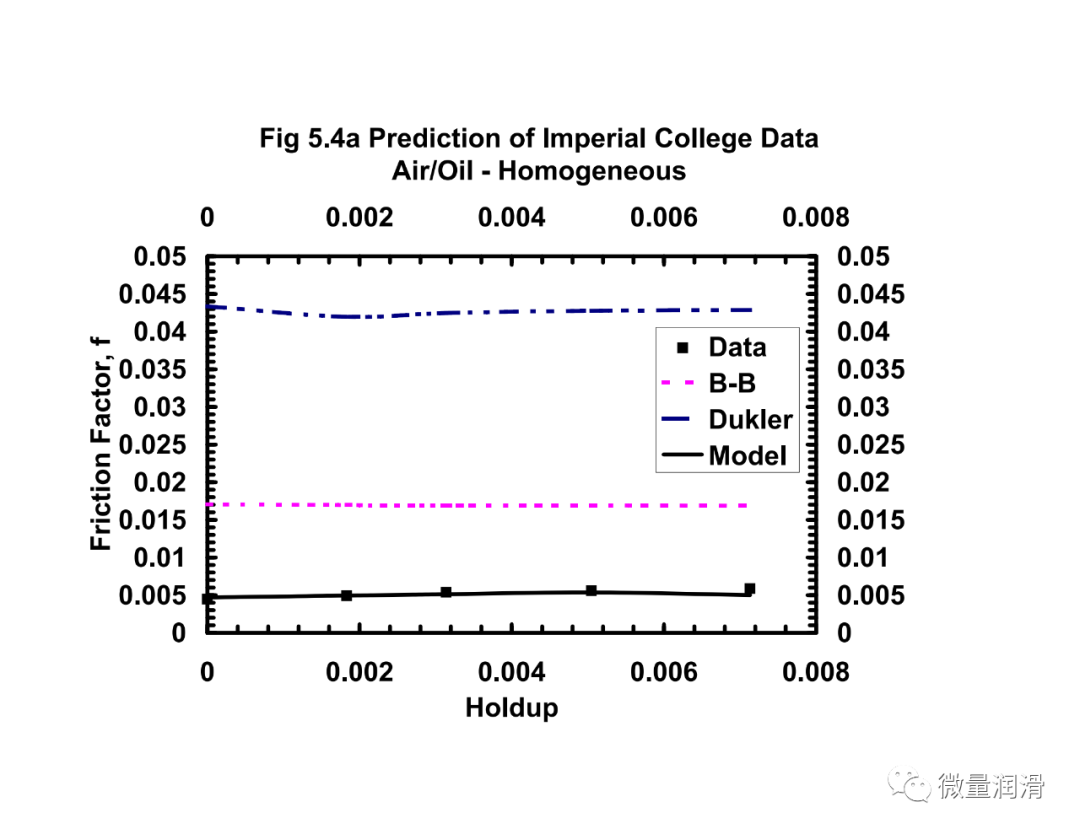
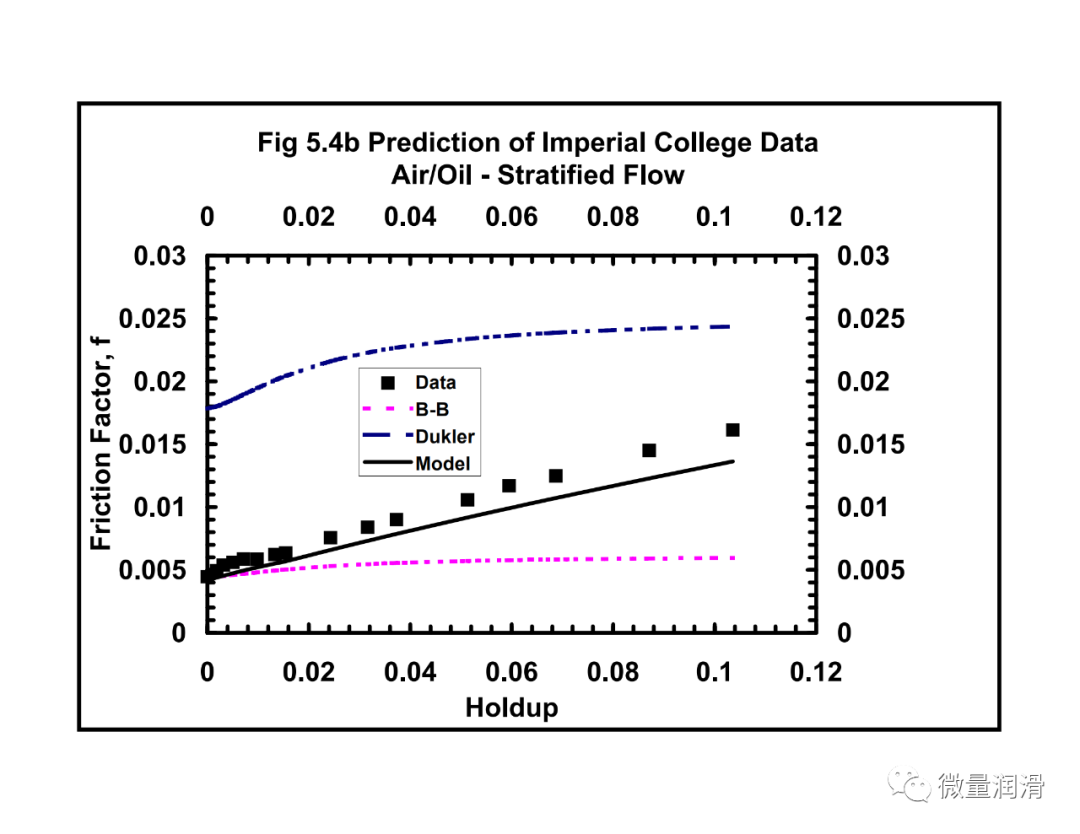
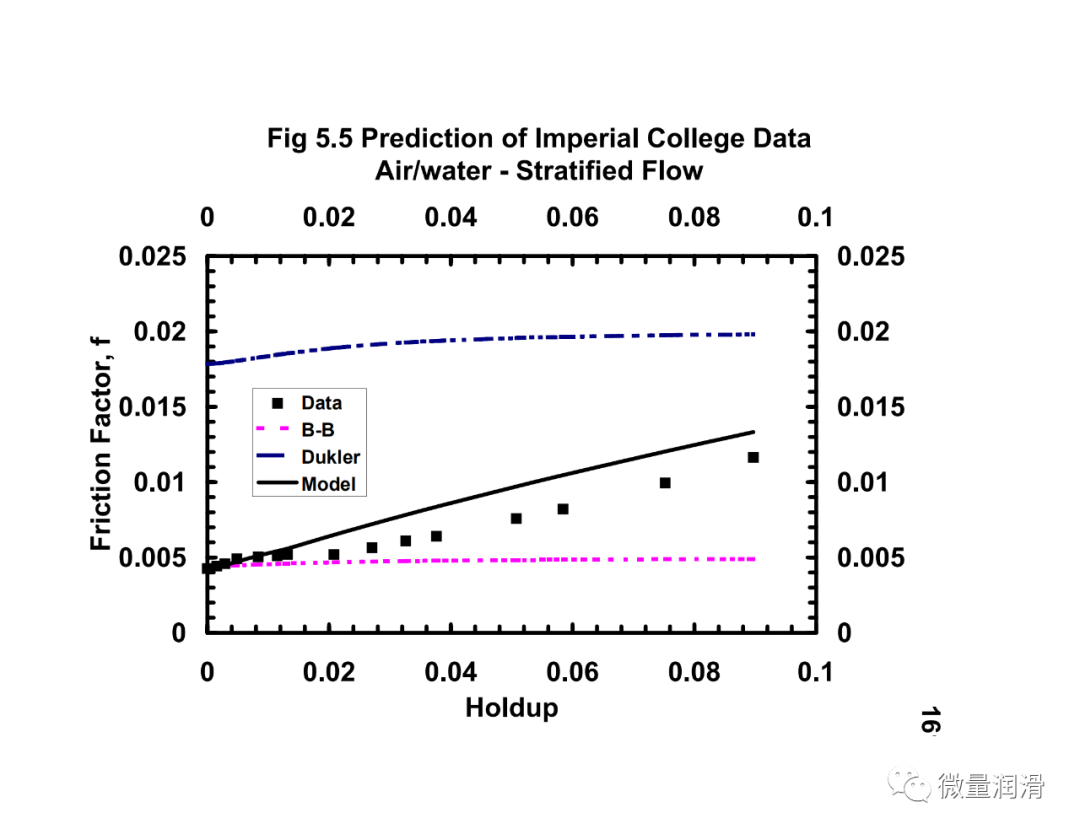
从本研究中得到了两个相关性:界面摩擦因子相关性和均匀摩擦因子相关性。这些相关性是从本研究中发展起来的集成均匀分层模型的关键组成部分。界面摩擦因子和均匀摩擦因子与现有相关性的比较见图5.1-5.5。综合17模型和其他现有模型的预测也使用实验和现场数据进行了比较。
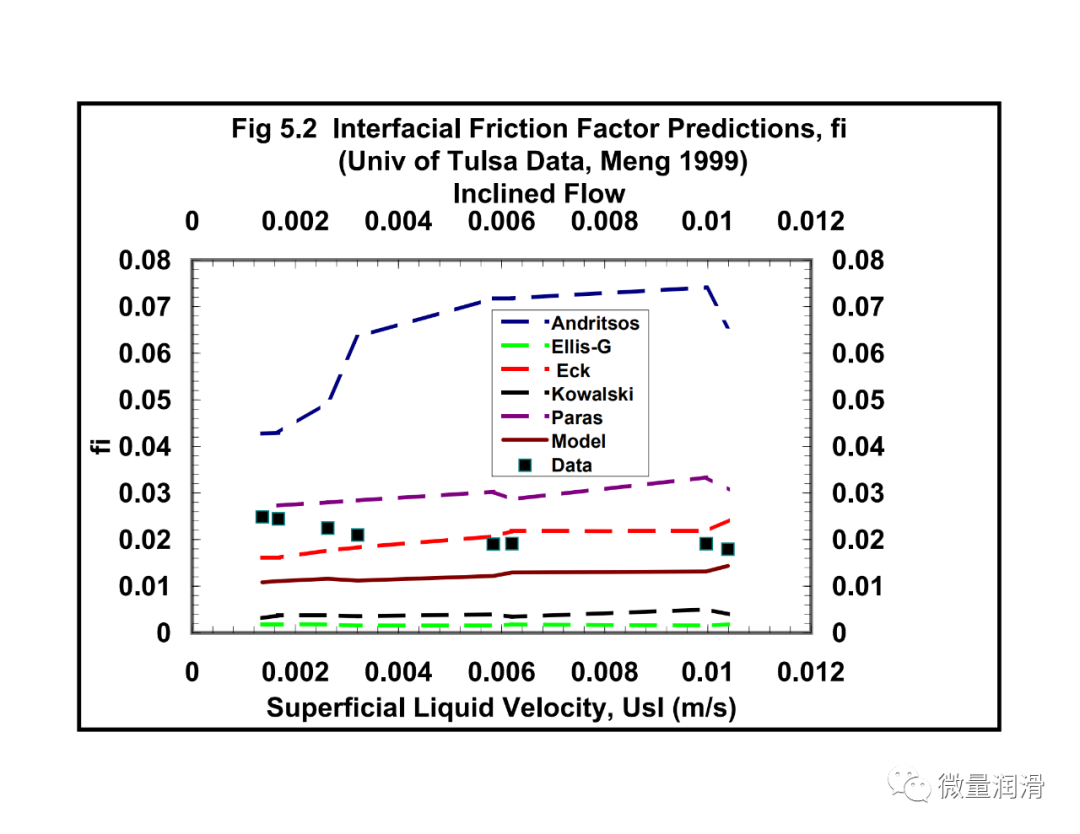
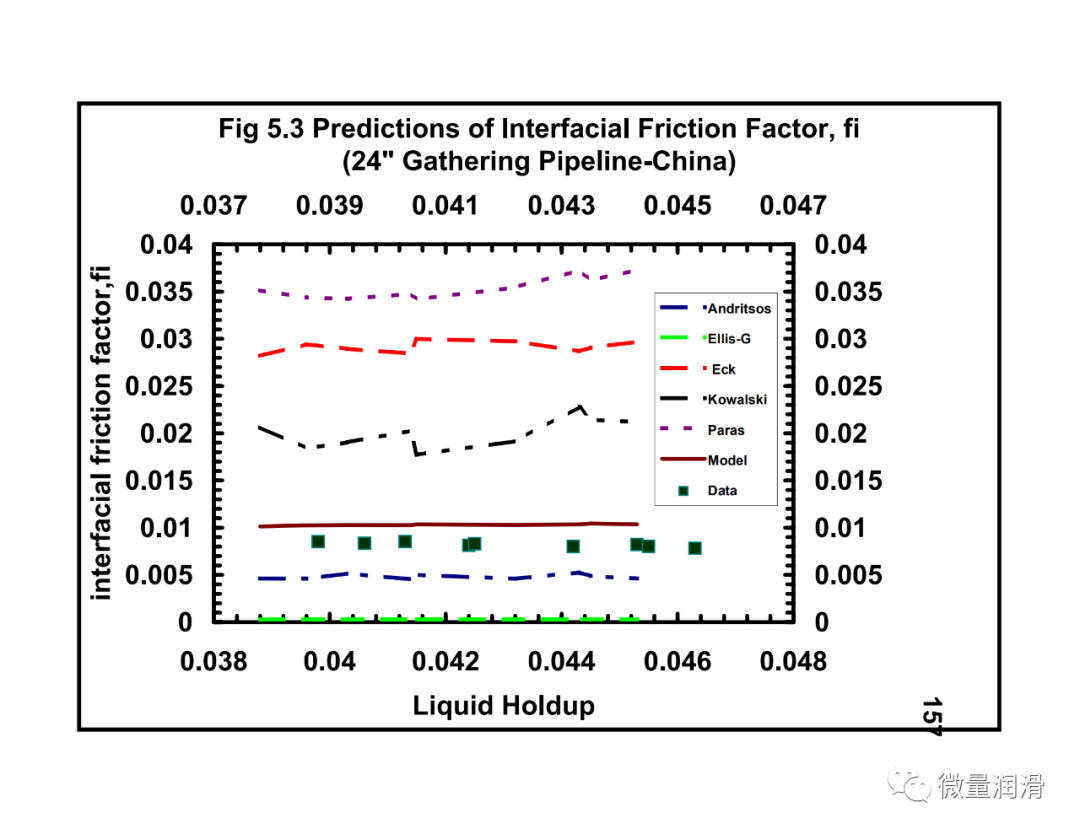
1. 拟议界面摩擦因子相关性检验
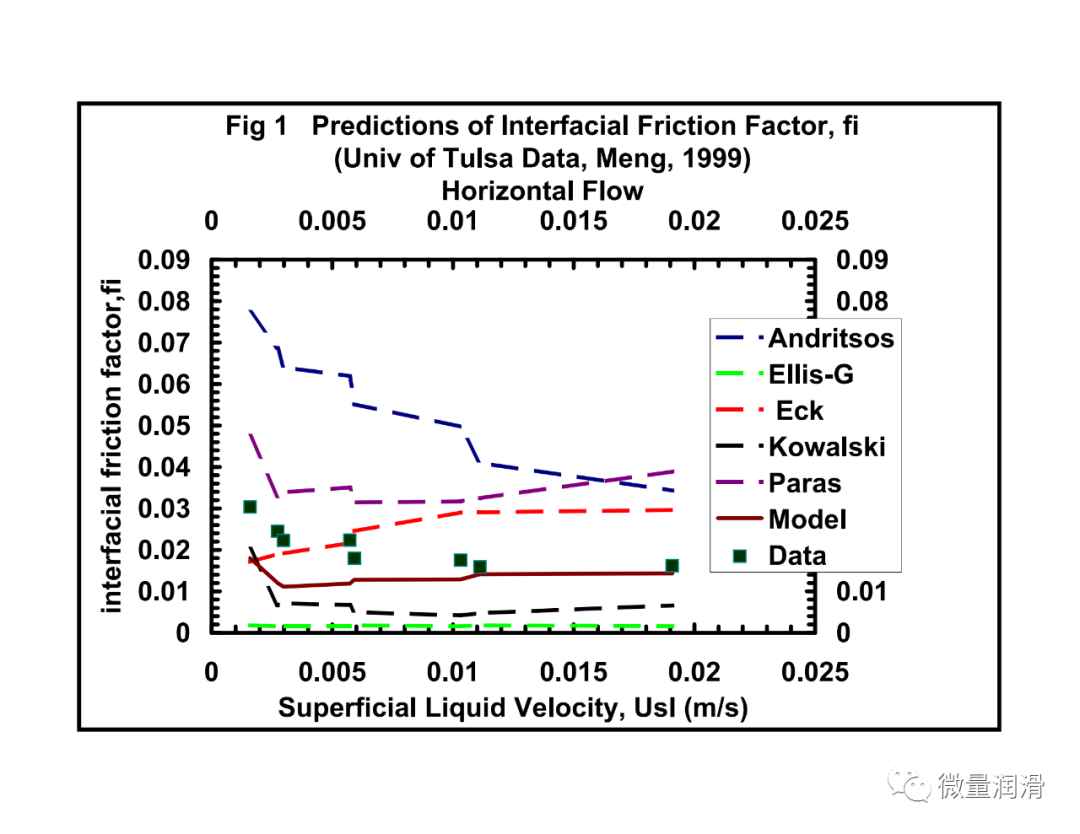
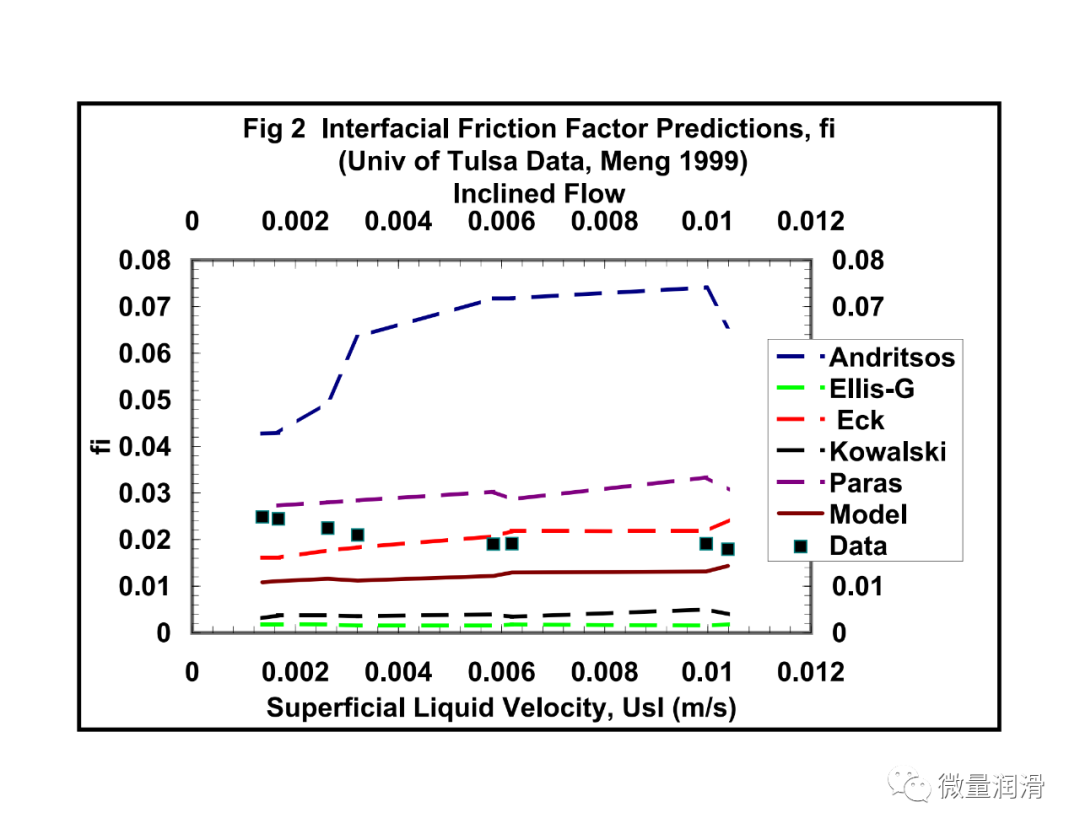
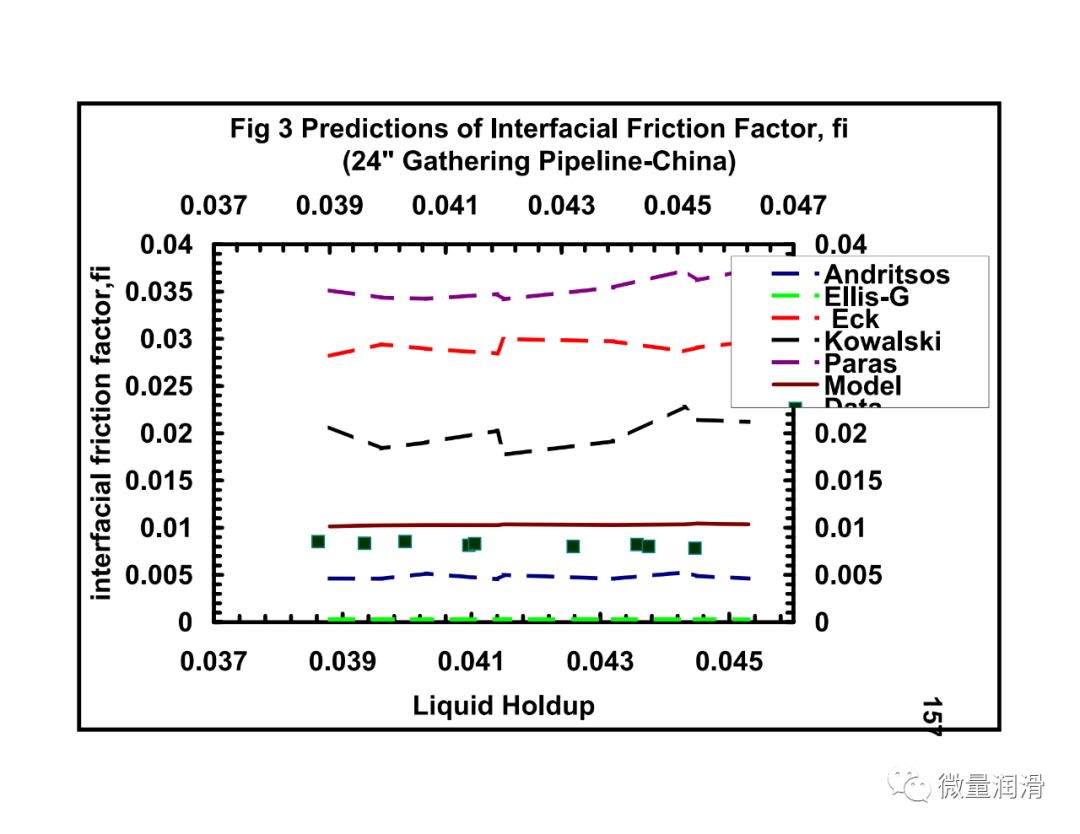
比较了界面摩擦系数与已有的界面摩擦系数的相关性。使用了塔尔萨大学流体流动项目的实验数据(Meng,1999年);阿尔维斯,1959年(数据来自斯坦福大学/卡尔加里大学多相流动数据库),以及从中国获得的实地数据(Asante等人,1993年。分析表明,与Eck/Hart等人、21%-256%、Ellis&Gay、90-96%、Andritsos等人、40%-252%、Kowalski、68%-145%和Paras等人、19-334%相比,该模型预测独立数据界面摩擦的误差在14%-40%范围内%。
表3建议的FI相关与现有相关性的比较。 (实验条件)
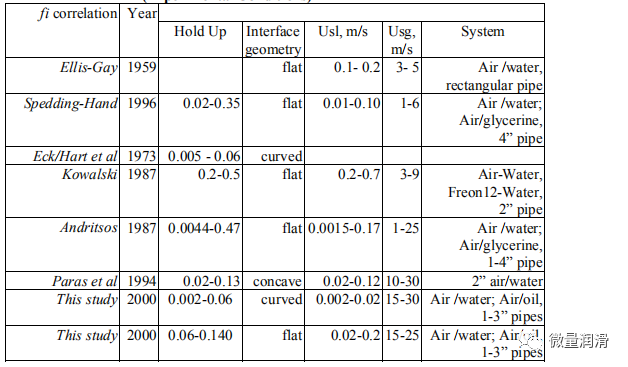
在预测中所显示的差异在很大程度上可以归因于本研究中考虑的低液体滞留量与其他研究相比。与大多数现有模型不同,与大多数现有相关性中考虑的高得多的保持率相比,感兴趣系统的液体保持率小于0.05。表3提供了一些现有的界面摩擦因子相关性的摘要,Paras等人的一组数据最接近本研究中所考虑的,但他们提出,界面摩擦因子仅随作为膜高度函数表示的液体雷诺数而变化。这与本研究和其他研究结果不同(Kowalski,1987年;Andritsos,1986年;Eck,1973年),其中考虑了气体雷诺数和滞留量的影响。现有的大多数相关性也假定了气液界面的“Taitel-Dukler”平面几何,而本研究的大多数观测结果表明了一个周向界面。此外,气体和低负荷液体系统的这种小含率通常产生薄膜(Paras等人,1996年,Hart等人,1987年)。与通常具有较高载荷的厚膜相比,在薄膜界面产生明显的大振幅波。
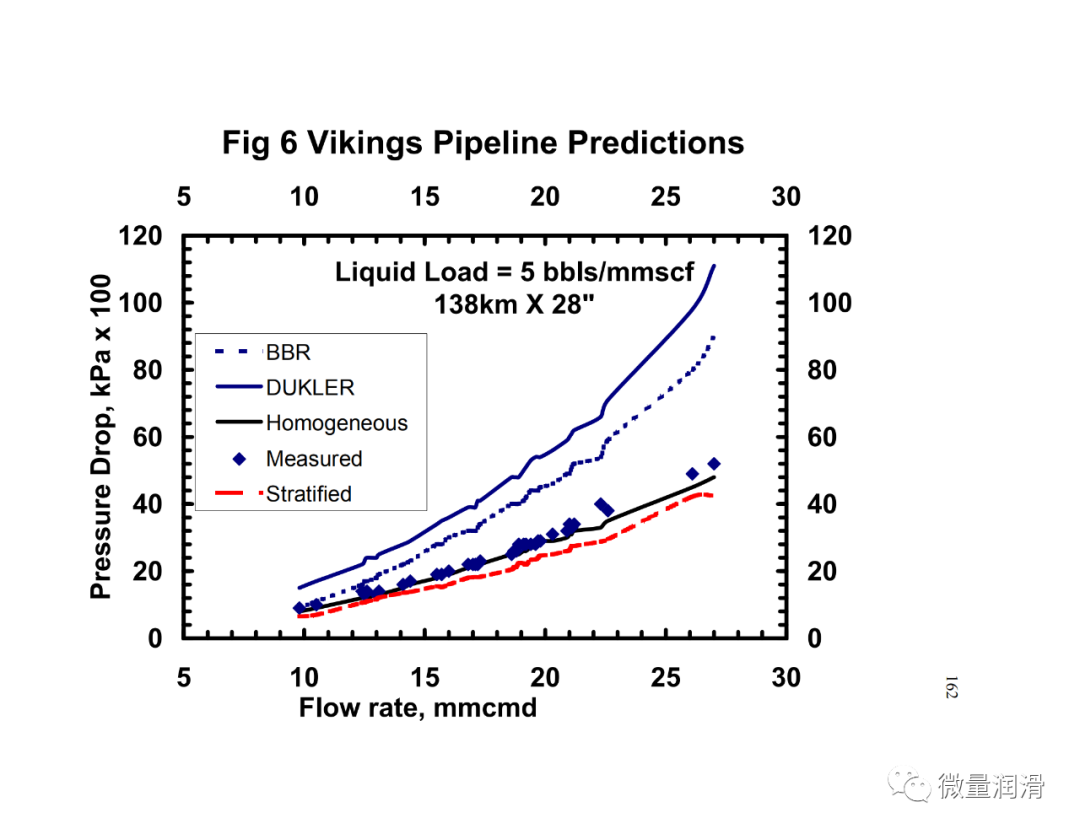
2. 现场数据集成模型测试
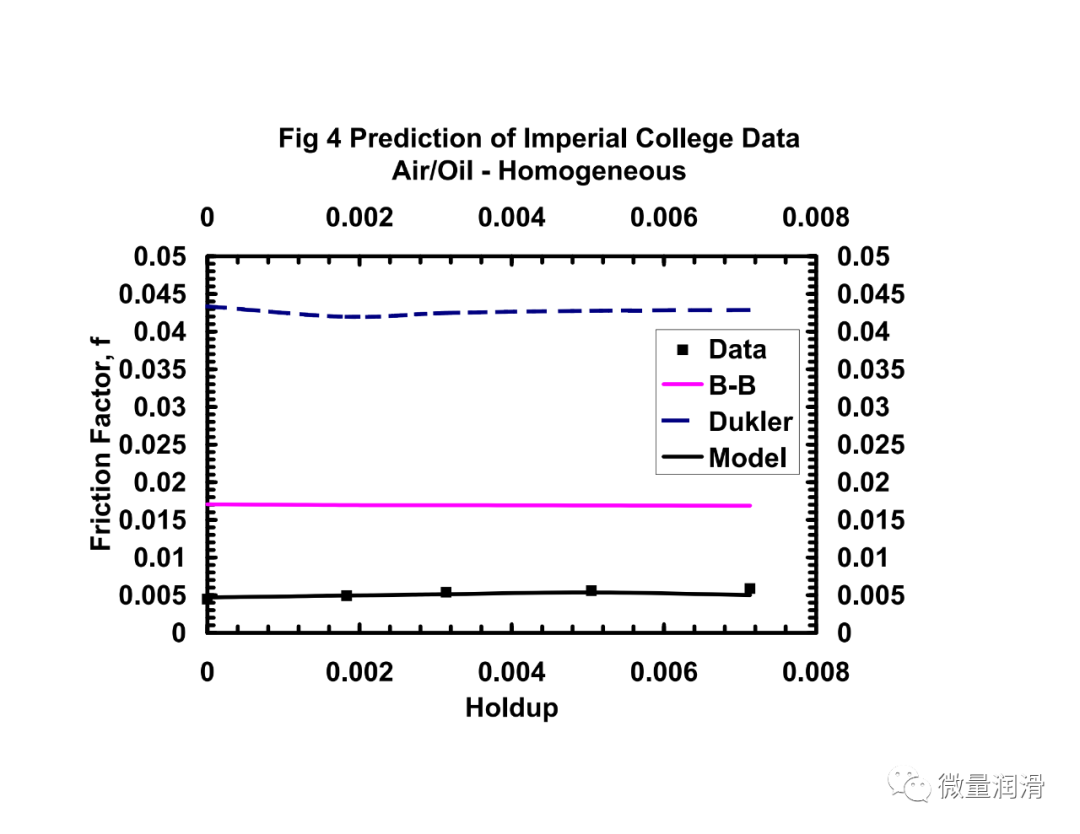
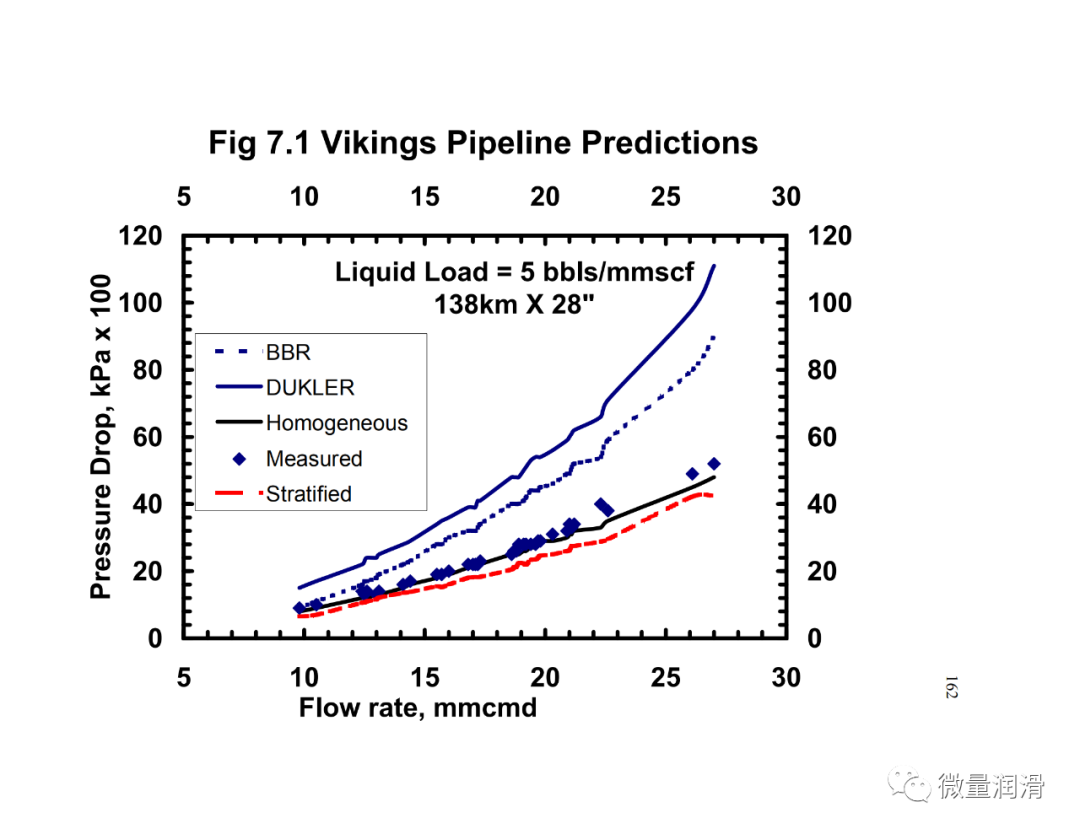
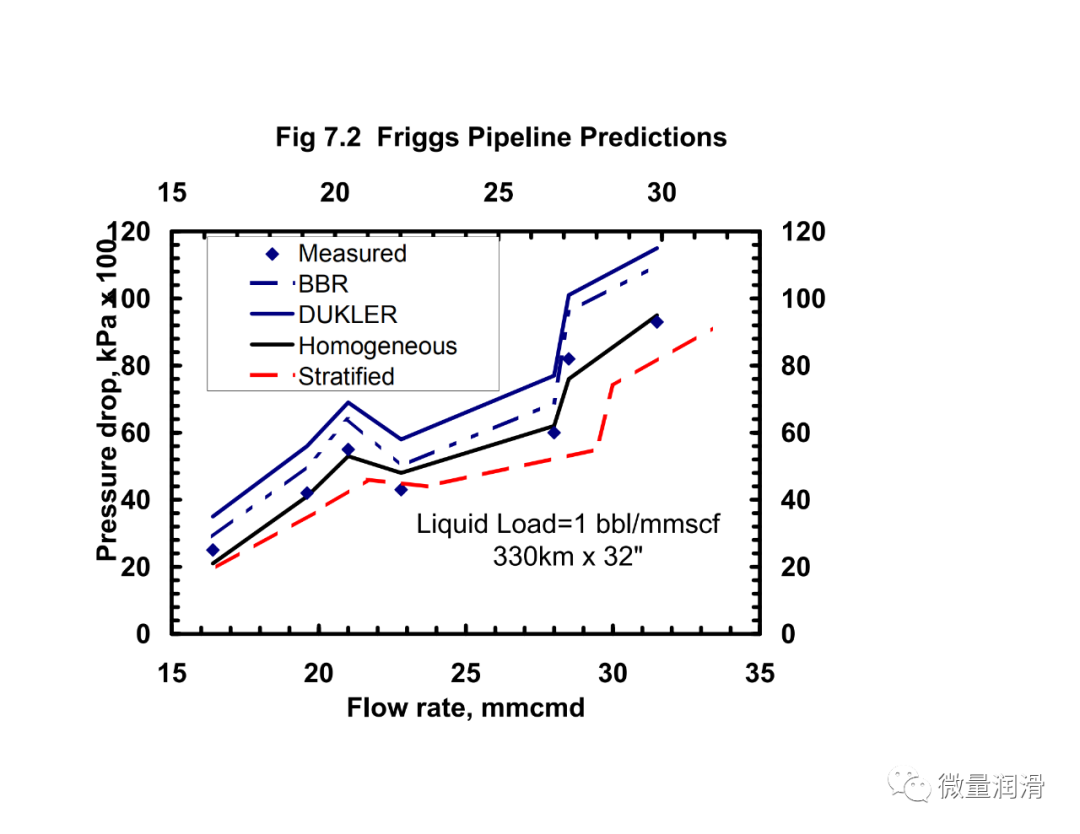
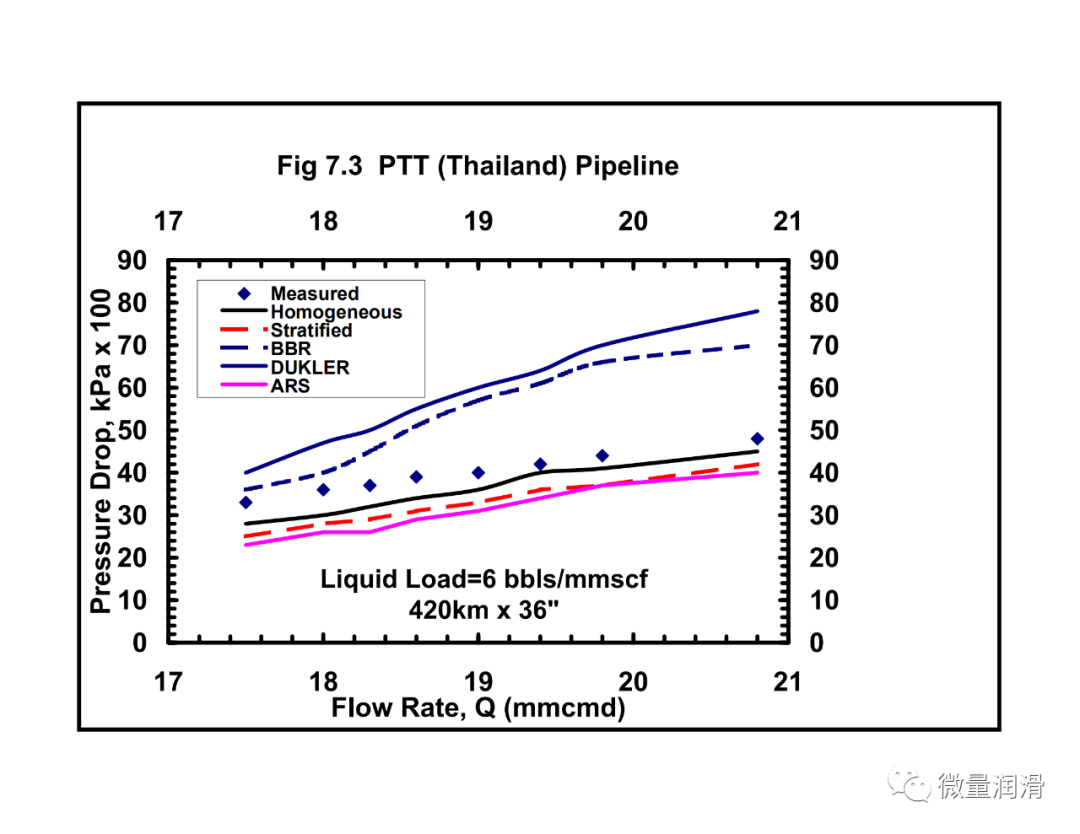
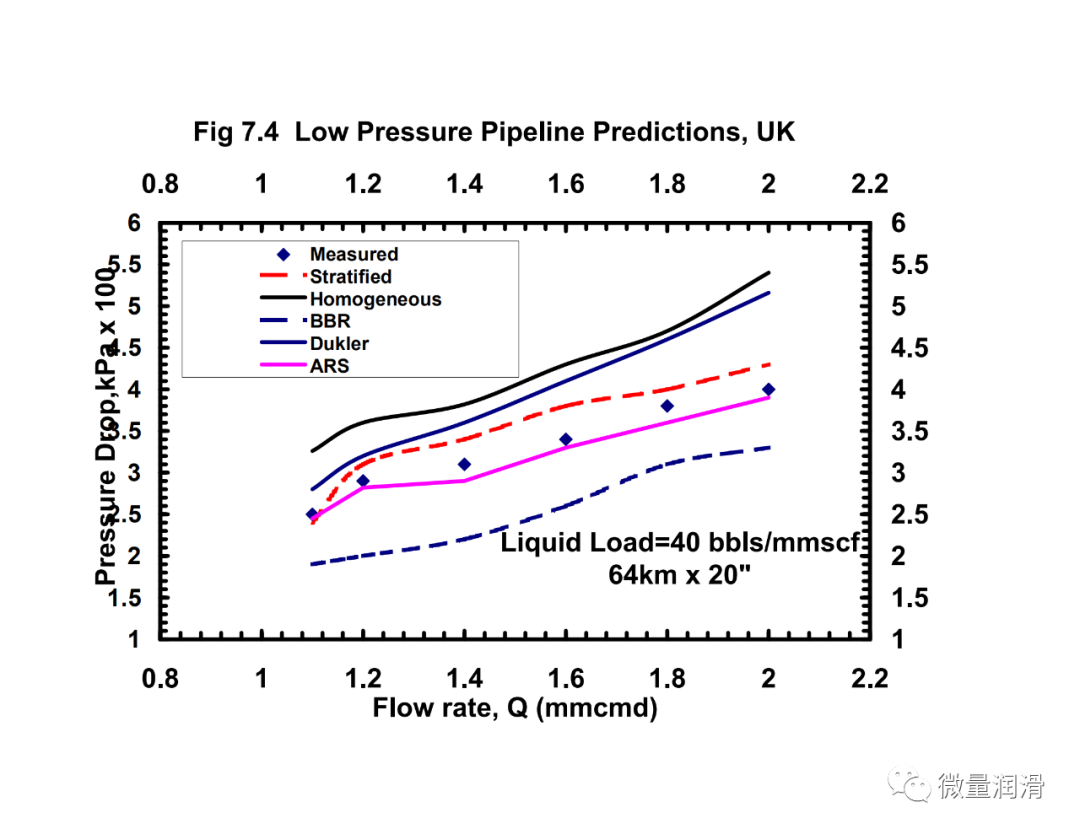
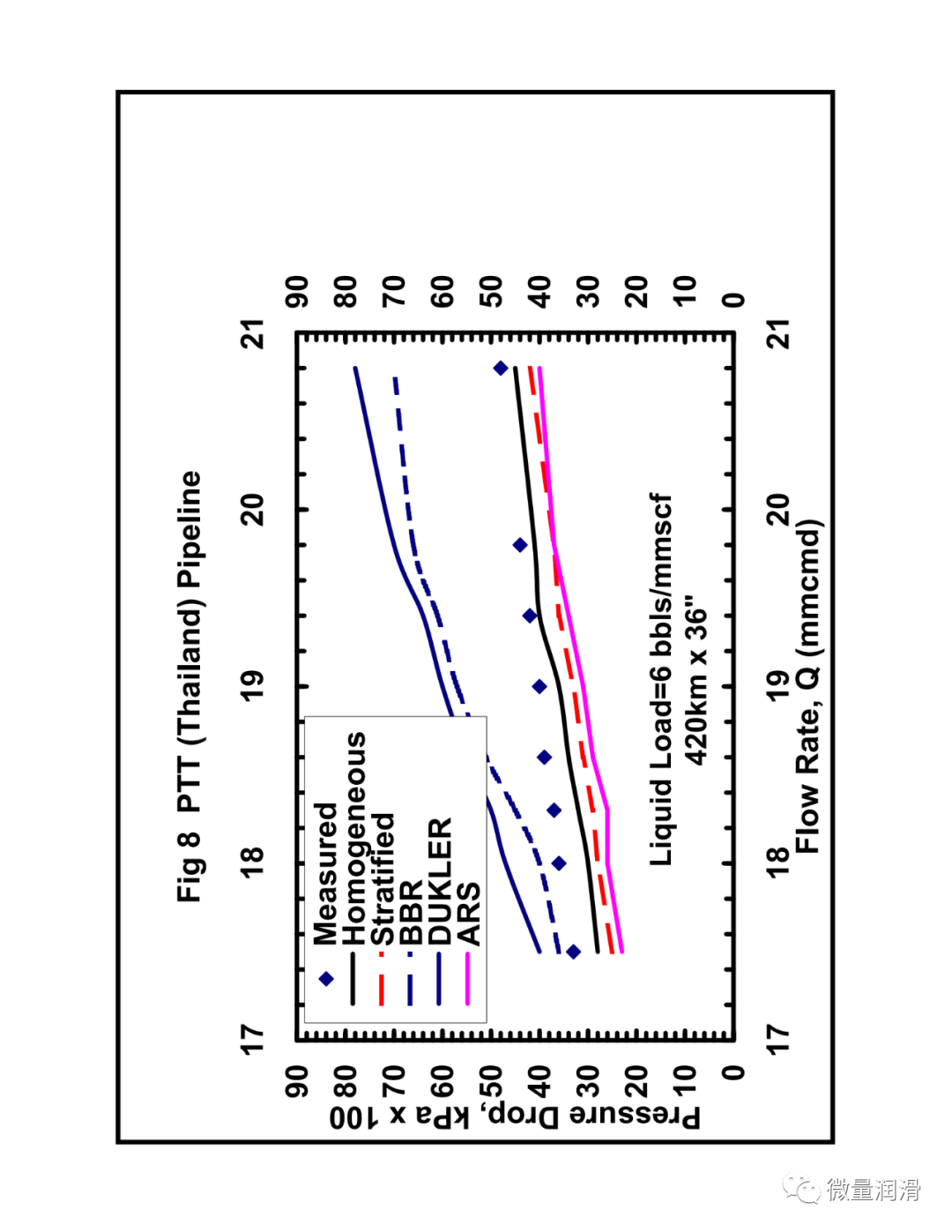
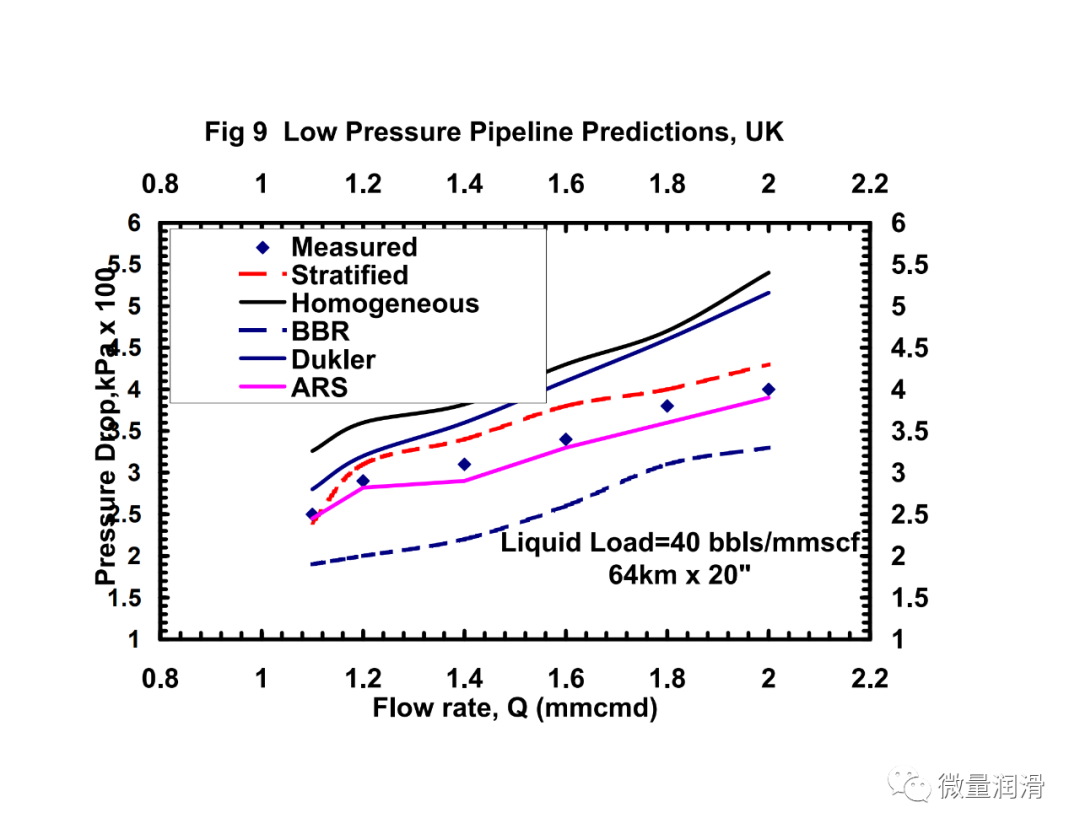
将该模型和行业中常用的其他两相关联的压降预测与从不同的传输和采集管道系统中获得的运行数据进行了比较。结果见图7.1-7.4。很明显,对于气体和低负荷液体系统(含率小于0.005),流动行为比两个不同相更接近均匀流动。对于维京管道(图7.1),均匀模型预测的百分比误差约为-10%,标准差为3.9,而Beggs和Brill两相模型预测的误差为45%,标准差为14.8。然而,对于较高的液体负荷,(图7.4)均匀模型的误差界为35%,而分层流动模型、Beggs和Brill相关和Dukler模型的误差界分别为11%、-23%和21。对于较高的液体负荷,通常在一些气体凝结水系统和一些收集管道(小于100bbls/mmscf)中看到,分层两相方法是可取的。Beggs和Brill和Dukler的相关性是经验的,基于液体负荷远高于本研究中所考虑的。用Neotec的Pipeflo软件计算现有关联式的压降,用Gregg工程软件程序和NOVA的Caspr程序计算模型的压降。这使得实际操作条件、海拔变化、传热计算和流体性质的变化可以很容易地沿管道进行模拟。
结论
气体和少量液体同时在管道中流动,与单相流动和高液体负荷的两相流动相比,具有非常不同的流动特性。根据本研究的实验结果以及现有文献,提出以下结论。
1) 对于气体和低负荷液体系统,液相以分散液滴和/或薄膜的形式传播。结果表明,对于这种体系,均相模型适用于含液率高达0.005。超过这个临界极限,流动将改变为分层状态。对于分层流动情况,对于中等的气液比(含率>0.06),界面是平坦的,对于高的气液比则是弯曲的。
2) 在气流中引入少量液体可以大大增加压降。在流型中,由于从一种流型向另一种流型的转变,压降随液体负荷的变化显著。将液体负荷的影响与压降联系起来需要定义液体的运输方式以及由于液体的存在而导致的传输因子的相对变化。
3) 已经建立了一个综合的均匀分层流动模型来预测气体系统和通常在气体传输和收集管道中看到的低负荷液体的传输特性。它解释了一个平面和弯曲的双重界面几何取决于液体负荷。与现有的两相模型不同,该模型假设完全粗糙流动时雷诺数上的摩擦因子是独立的。高压燃气管道通常是如此。
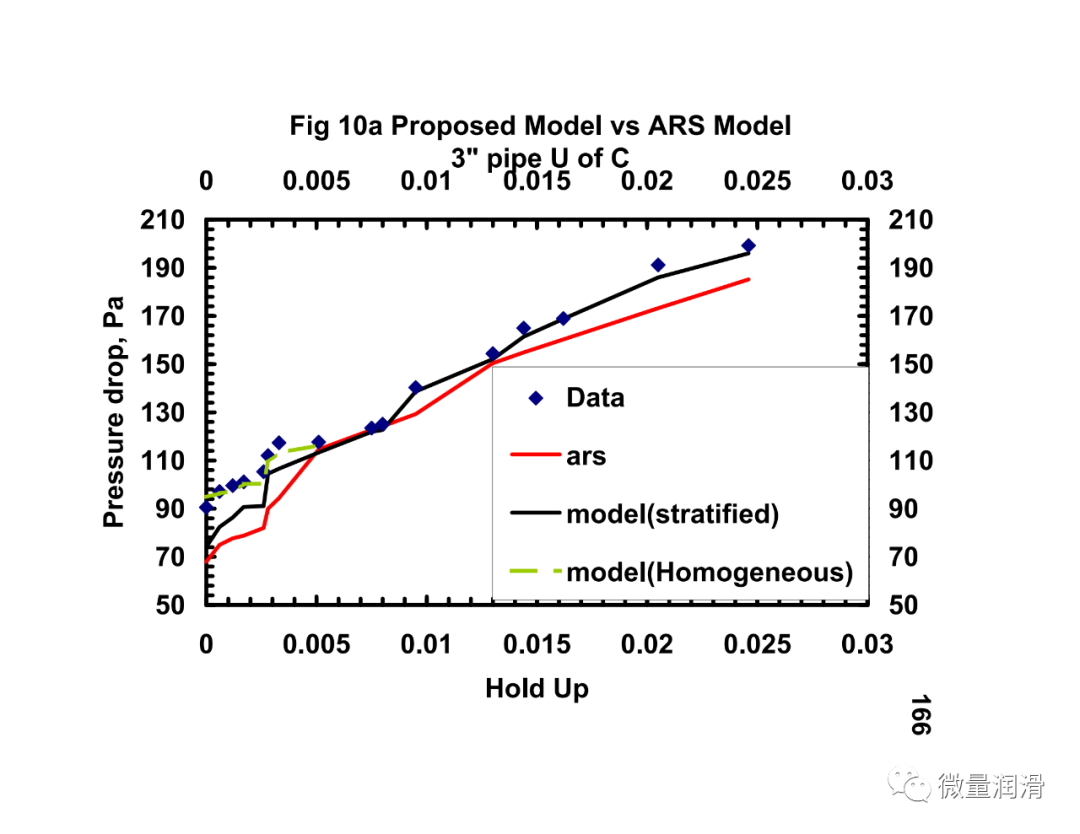
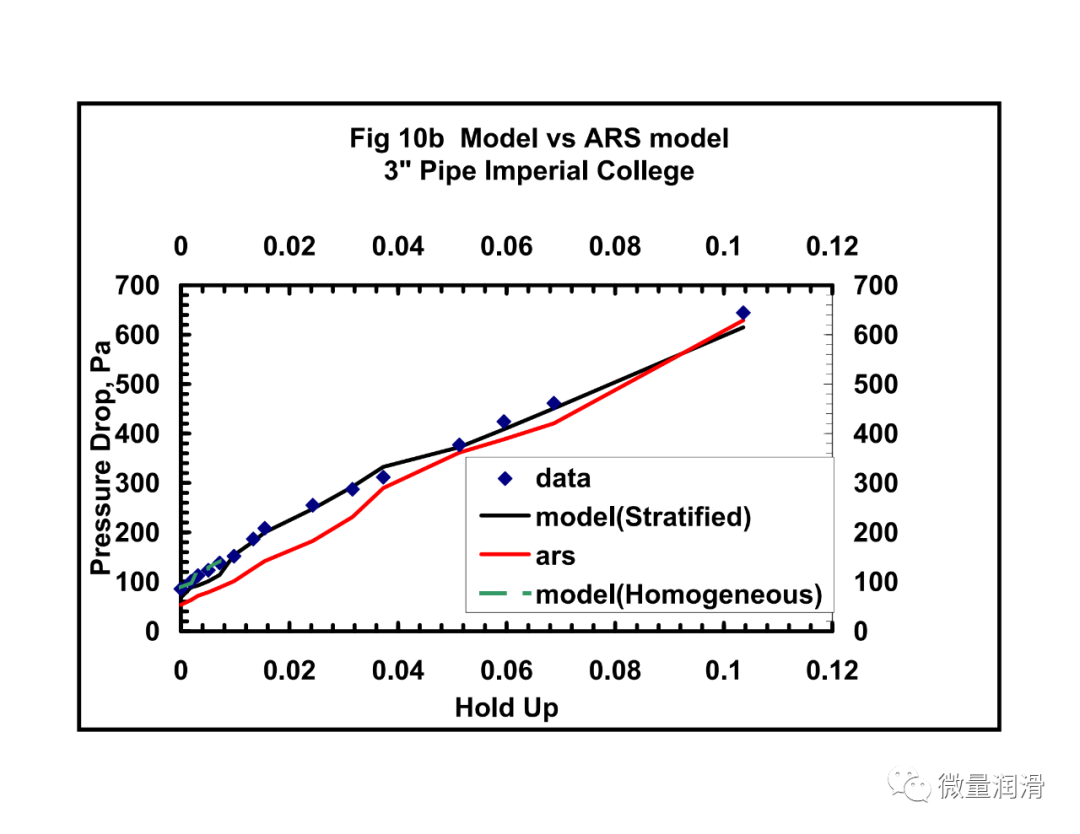
4) 该模型还代表了对Hart和Hammersma的表观粗糙表面(A RS)模型的改进,特别是对于低含液量(<0.006)。对于这种液体滞留,所提出的模型的均匀分量比ARS模型提供了更好的预测。
5) 还发展了一种基于低液体载荷的具有代表性的界面摩擦因子相关。这种相关性将气体和液体雷诺数以及液体保持率和膜厚(或高度)与界面摩擦因子联系起来。
6) 提出了一种基于含阻力的均匀摩擦系数相关方法,该方法调整了光滑管道方程,以考虑气体和低负荷液体的均匀流动。